Eberick – Pilar com Mais Aço na Cobertura
Intuitivamente, imaginamos que quanto maior for a carga vertical atuante em um pilar maior a quantidade de armadura que será necessária, certo? No entanto, por vezes nos deparamos com a situação abaixo, onde o pilar com maior taxa de armadura é justamente aquele que recebe a menor carga. Sabe porque isso acontece?
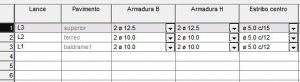
Um dos principais motivos é que, para cargas baixas, aumentar a força axial pode AUMENTAR A RESISTÊNCIA DO PILAR – ao invés de diminuir. Consequentemente, o pilar do penúltimo lance pode ter momentos resistentes superiores ao pilar do último lance. Duvida? Veja abaixo alguns exemplos desse fenômeno em prática simulados através do Eberick.
Antes de prosseguir para as simulações talvez seja interessante ler este artigo onde eu explico como funciona o cálculo da linha neutra para pilares.
Conheça Todas As Minhas Estratégias para Otimizar Pilares no Eberick
SIMULAÇÕES
As simulações abaixo foram feitas em um pilar com seção de 20×35, com fck 25 MPa e armado com 4 barras de 10mm. Os momentos fletores atuantes na seção foram sempre os mesmos. Variou-se apenas o esforço axial característico “N”.
Interessante também observar o movimento da linha neutra a medida em que a força de compressão foi aumentada.
Simulação 1: N = 0KN
- Mrd,x = 10,84KN.m
- Mrd,y = 3,61 KN.m
No cenário inicial há apenas a ação dos esforços de flexão. Observa-se que o momento resistente da seção é equivalente a metade do momento soliciante.

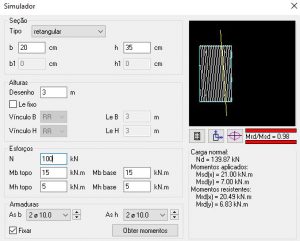
Simulação 2: N = 100KN
- Mrd,x = 20,49KN.m
- Mrd,y = 6,83 KN.m
Na simulação 2 foi acrescentado um esforço axial de compressão de 100KN. Percebe-se que os momentos resistentes da seção quase dobaram em relação ao cenário anterior. Por si só, esse exemplo já ilustra a afirmação que eu fiz no início desse artigo de que, para pilares com cargas baixas, aumentar o esforço axial aumenta a resistência. Mas vamos prosseguir com as análises.
Simulação 3: N = 200KN
- Mrd,x = 27,89KN.m
- Mrd,y = 6,98 KN.m
Na simulação 3 o esforço axial adotado foi de 200KN e, novamente, obtivemos um aumento significativo nos momentos resistentes da seção. Dessa vez eles estão praticamente iguais aos esforços soliciantes.

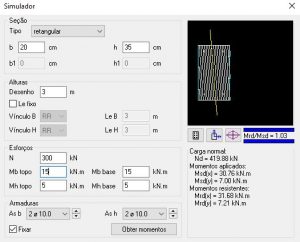
Simulação 4: N = 300KN
- Mrd,x = 31,68KN.m
- Mrd,y = 7,21 KN.m
Aumentando o esforço axial característico para 300KN houve novo acréscimo de resistência na seção sendo que, dessa vez, os momentos resistentes superaram os momentos soliciantes e a seção está “passando” no dimensionamento.
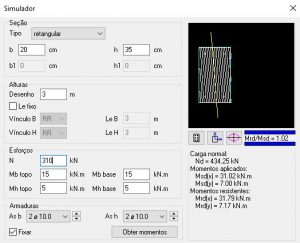
Simulação 5: N = 310KN
- Mrd,x = 31,79KN.m
- Mrd,y = 7,17 KN.m
Aumentando N para 310KN percebe-se um novo acréscimo nos momentos resistentes, mas observe que a relação Mrd/Msd diminui em relação ao exemplo anterior! Isso quer dizer que o acréscimo de esforço axial da simulação 4 para a simulação 5 gerou maior acréscimo de esforço solicitante do que acréscimo de esforço resistente. Isso indica que estamos próximos ao “ponto de inflexão”, ou seja, estamos chegando perto do ponto a partir do qual aumentar o esforço normal vai diminuir a resistência da peça.
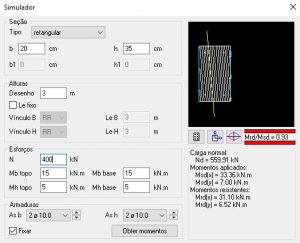
Simulação 6: N = 400KN
- Mrd,x = 31,1KN.m
- Mrd,y = 6,52 KN.m
Como esperado, na simulação 6 observa-se que o acréscimo de esforço normal começou a provocar redução nos momentos resistentes e a seção já nem está mais passando.
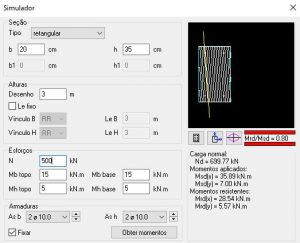
Simulação 7: N = 500KN
- Mrd,x = 28,54KN.m
- Mrd,y = 5,57 KN.m
Aumentando novamente a carga, a situação ficou ainda mais crítica.
Quer entender porque isso acontece? Conheça o curso Otimização de Pilares no Eberick.




