Eberick – Simulador de Pilares

Para o cálculo de vigas, podemos obter manualmente a posição da linha neutra, com essa informação obtemos a área de aço. Entretanto, para o cálculo manual de pilares geralmente recorremos à ábacos e à tabelas, por isso não adquirimos o mesmo “sentimento” para a relação entre a linha neutra, a área de aço e o momento resistente que temos quando calculamos vigas.

LINHA NEUTRA DOS PILARES

Como assim, pilar tem linha neutra? Nunca calculei linha neutra para pilar?

O cálculo da linha neutra está “embutido” no ábaco e na tabela e é inviável e ser obtido manualmente.

Para vigas, há apenas flexão em uma direção, logo sabemos de antemão que a linha neutra é horizontal, basta apenas descobrir a profundidade dela na seção da viga.

No entanto, como o pilar está sujeito à esforço normal e à flexão em duas direções, além de profundidade, também precisamos descobrir o ângulo de inclinação da linha neutra. É importante saber também a disposição da armadura na seção.

Vamos ver abaixo alguns exemplos para entender melhor como isso funciona. Para ilustrar pegarei dois pilares de 15×30, um armado com 6 barras de 10mm e outro com 4 barras de 12.5mm. Escolhi essas duas configurações pois ambos contém aproximadamente a mesma quantidade de aço, mudando apenas a disposição dessa armadura na seção.

Consultando as tabelas úteis para detalhamento de estruturas encontramos a área de aço de cada bitola:

• 6 barras de 10mm 6 x 0,785cm² = 4,71cm²
• 4 barras de 12.5mm 4 x 1,22cm² = 4,88cm²

Com isso, temos uma diferença de 3,6% na quantidade total de aço.

SIMULADOR DO EBERICK

As análises serão realizadas a partir do simulador de cálculo de pilares do Eberick mostrado abaixo. Nele podemos definir o tipo e as dimensões da seção, o comprimento de flambagem, os esforços solicitantes com seus valores característicos e, por fim, as armaduras, como podemos ver abaixo:

No lado direito, vemos o resultado do cálculo apontando a relação entre o esforço resistente e o solicitante (Mrd/Msd) e os respectivos momentos de cálculo e momentos resistentes. Na imagem vemos também a seção, a locação das armaduras e a posição da linha neutra (linha em amarelo).

PARE de Deixar o Eberick SUPERDIMENSIONAR Seus Pilares!

PRIMEIRA SIMULAÇÃO

Na primeira simulação, a seção está solicitada por uma força normal de 150KN e um momento de 15KN.m no topo e na base, na direção de maior inércia do pilar.

a) Para a configuração com 4 barras de 12.5 temos uma folga de 5% (Mrd/Msd = 1,05) do esforço resistente em relação ao esforço solicitante de cálculo.

Repare que a linha neutra está praticamente cruzando com duas barras, as quais praticamente não contribuirão para a resistência desse pilar. A única barra que está contribuindo para combater os esforços de tração é a barra inferior esquerda.

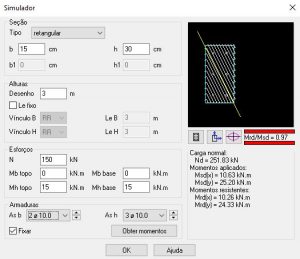
b) Para a configuração com 6 barras de 10.0, vemos que a relação Mrd/Msd deu 0,97, logo a seção não é capaz de resistir aos esforços solicitantes.

Mais uma vez, observa-se que temos várias barras próximas à linha neutra. A zona de tração é a região inferior esquerda. Há três barras nessa região, sendo que duas delas estão próximas à linha neutra e contribuem pouco. Novamente, apenas a barra no canto inferior esquerdo contribui efetivamente para combater a tração, diferentemente do caso “a” essa barra tem agora 10mm, logo a eficiência dessa configuração será menor do que no caso anterior. Isso explica a diferença de 8%.

SEGUNDA SIMULAÇÃO

Na segunda simulação mudaremos os esforços solicitantes, agora teremos 5 KN.m de momento fletor atuando no topo e na base em ambas direções.

a) Para a solução com 4 barras de 12.5: Mrd/Msd = 1,01. A zona tracionada é a região à esquerda da linha neutra. Temos duas barras nessa região.

b) Enquanto para a solução com 6 barras de 10mm: Mrd/Msd = 0,99. Para essa configuração, temos 3 barras na região tracionada.

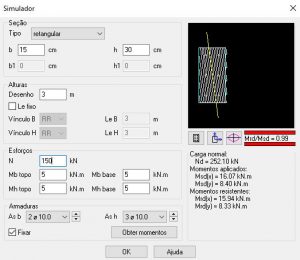
Percebe-se que, ao alterar os momentos atuantes, a inclinação da linha neutra mudou. Agora, inclusive, as barras já não estão mais tão próximas da linha neutra como na simulação anterior, com isso conseguimos um melhor aproveitamento da armadura na seção.

De fato, a distribuição do caso b está, dessa vez, melhor que a distribuição do caso a e, por conta disso, a seção com 6 barras de 10mm resiste apenas 2% menos que a barra com 4 barras de 12.5mm, apesar da primeira ter 3,6% menos aço do que a segunda.

Descubra métodos avançados para Otimizar Seus Pilares no Eberick!